诸君安。之前小编给大家分享过如何用stata数学函数处理数值型数据 (Stata数学函数总结（一）)，您是否掌握了呢？如果觉得还不过瘾，没问题，小编这就为大家双手奉上Stata数学函数总结（二），方便大家更好地运用Stata。

一、factorial & gamma函数

1、lnfactorial(n)---返回n阶乘的自然对数

注 意：求n阶乘的对数比单纯求阶乘更有用，因为存在溢出值问题。对于factorial(n)，当n>170时，返回缺失值，而对于 lnfactorial(n)，当n> 1e+305时，才会返回缺失值，所以lnfactorial(n)能计算更大的数值，在一定程度上可以避免溢出值的问题。

例子说明：

生成一组数据：

clear

set obs 10

gen num = round( 200 * uniform() )

计算num的阶乘以及阶乘的对数：

gen double v1=exp(lnfactorial(num))

gen v2 = lnfactorial(num)

结果如下：

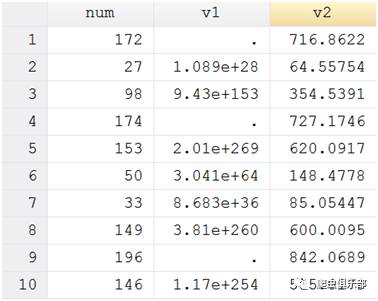
其中，v1的存储类型是double，而v2的存储类型为float，但是当n>170时，v1就返回缺失值，说明求n阶乘的对数比单纯求阶乘更有用，lnfactorial(n)能计算更大的数值。

2、lngamma(x)--返回gamma函数的自然对数

(1)简单介绍一下gamma函数，伽玛函数(Gamma函数)，也叫欧拉第二积分，是阶乘函数在实数与复数上扩展的一类函数。伽玛函数（Gamma Function）作为阶乘的延拓，是定义在复数范围内的亚纯函数，通常写成Γ(x)。

在实数域上伽玛函数定义为：

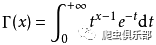
在复数域上伽玛函数定义为：

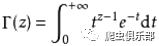
(2)lngamma(x)，如果x是一个实数，则返回值为ln(abs(gamma(x)))，如果x为复数，返回值为ln(gamma(x))。

例子说明：

lngamma(-2.5)=-0.056244

lngamma(-2.5+0i)=0.056244+3.1416i

(3)gamma函数有一性质为：当参数x是正整数时，函数的值就是前一个整数的阶乘。所以当x为正整数时，lngamma(x)=ln((x-1)!)=lnfactorial(x-1)。如果x<0（这里x不能为负整数，如果x为负整数，返回值为缺失值），返回的是一个数值。所以，我们可以用 exp(lngamma(x))来得到gamma(x)函数的绝对值。

在stata中，我们可以利用exp(lnfactorial(n))函数求n的阶乘，但是n必须为正整数，事实上，小数也有阶乘，我们可以利用gamma函数计算小数的阶乘。

当n为小数时：

n>0，n!=gamma(n+1)=n*(n-1)!

n<0，n!=gamma(n+1)

例子说明：

调用sp500.dta里面的一组数据change，并计算change的阶乘：

clear

sysuse sp500.dta

keep change

keep in 15/25

sort change

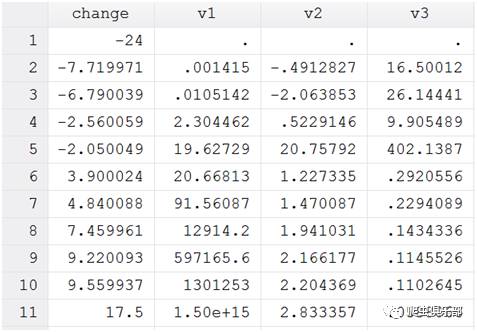
gen v1 = exp(lngamma(change+1))

结果如下：

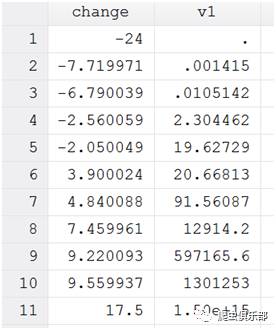
v1就是change的阶乘，需要注意的是负整数的阶乘为无穷大，所以负整数的阶乘是没有意义的。

(4)我们也可以利用gamma(x)和exp(x)的组合解决一些问题。

例子说明：

计算 Β(a,b) = Γ(a) Γ(b) / Γ(a + b)的值：

程序：

exp(lngamma(a) +lngamma(b) - lngamma(a + b))

式中的参数(a,b)可以是数字、变量或者表达式。

3、digamma(x)--返回lngamma(x)的一阶导数

4、trigamma(x)--返回lngamma(x)的二阶导数

例子说明：

gen v2=digamma(change)

gen v3=trigamma(change)

结果如下：

二、reldif(x,y)函数

reldif(x,y)返回x,y的相对差异值，即：

reldif(x,y)=|x-y|/(|y|+1)

如果x和y都是相同类型的缺失值，则返回值为0；如果只有一个为缺失值或x,y为不同类型的缺失值，则返回缺失值。

例子说明：

reldif(15,7)=|15-7|/(|7|+1)=1  

reldif(., .) == reldif(.a, .a) == ... == reldif(.z, .z) == 0

reldif(.,.a) == reldif(., .z) == ... == reldif(.y, .z) == .

实例说明：

导入stata系统数据sp500.dta（为了方便观察，我们只列出前10个观测值）：

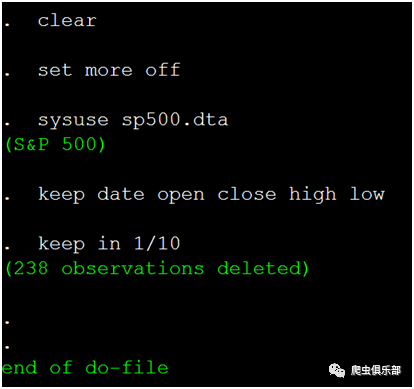
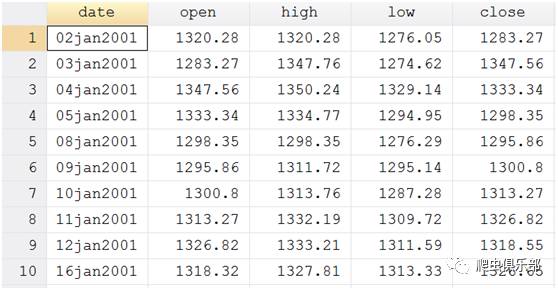
分别计算open（开盘价）和close（收盘价）以及high（最高价）和low（最低价）的相对差异值：

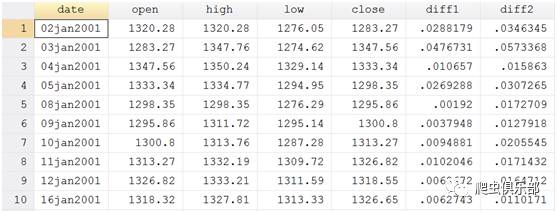
gen diff1=reldif(open,close)

gen diff2=reldif(high,low)

结果如下：

三、与符号相关的函数

1、abs(x)--返回x的绝对值

例子说明：

abs(-1)=1  

abs(10)=10

2、sign(x)--返回x的符号

x为负数，返回值为-1；x为正数，返回值为1；x为0，返回值为0；x为缺失值，返回值为缺失值。

例子说明：

sign(-3)=-1

sign(3)=1

sign(0)=0

sign(.)=.

实例说明：

导入系统数据sp500.dta：

clear

sysuse sp500.dta

keep date open close

keep in 1/10

生成一个变量diff，表示收盘价与开盘价的差：

gen diff=close-open

分别计算diff的绝对值和对应的符号：

gen v1=abs(diff)

gen v2=sign(diff)

结果如下：

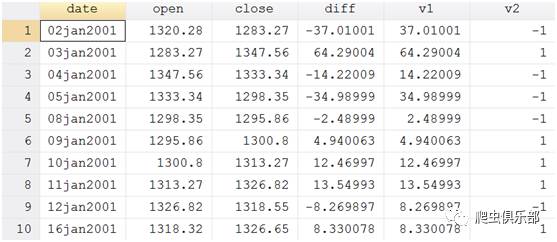
我们可以看到，当v2=1时，说明收盘价大于开盘价；当v2=-1时，收盘价低于开盘价。我们也可以直接通过gen v3=sign(close-open)来得到开盘价与收盘价的相对大小。

3、quadrant--返回复数所对应的象限

对应关系如下表：

例子说明：

quadrant(1+0i)==1

quadrant(-1+0i)==3

quadrant(0+1i)==2

quadrant(0-1i)==4

四、Logits,odds & related

1、cloglog(x)--返回ln{-ln(1-x)}的值。x的范围为（0,1）

2、invcloglog(x)--返回 1 - exp{-exp(x)}的值。[cloglog(x)的反函数]

3、logit(x)--返回ln{x/(1-x)}的值。x的范围为(0,1)

4、invlogit(x)--返回exp(x)/{1+exp(x)}的值。[logit(x)的反函数]

例子说明：

在stata中输入一个变量num：

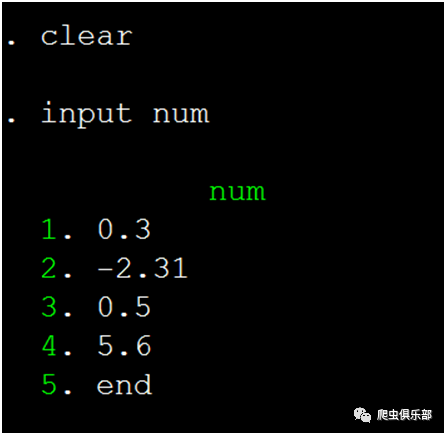
genv1=cloglog(num)

genv2=invcloglog(num)

genv3=logit(num)

genv4=invlogit(num)

结果如下：

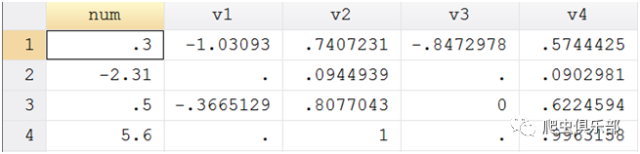
comb(n,k)返回从n中取k个元素的所有组合的个数，即：

comb(n,k)=n!/{k!(n-k)!}

(n,k都为整数，n>=1,k>=0且n>=k)

例子说明：

生成两组数据：

clear

set obs 10

gen v1=round(10+10*uniform())

gen v2=round(10*uniform())

计算comb(v1,v2)：

gen combnum=comb(v1,v2)

结果如下：

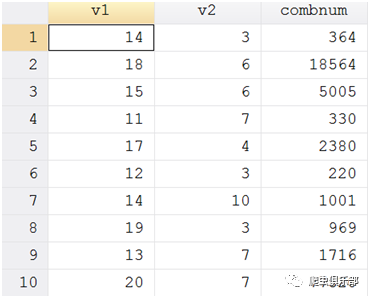
分享了Stata数学函数

现在

我们关注一下空气质量地图

总的空气质量如下图

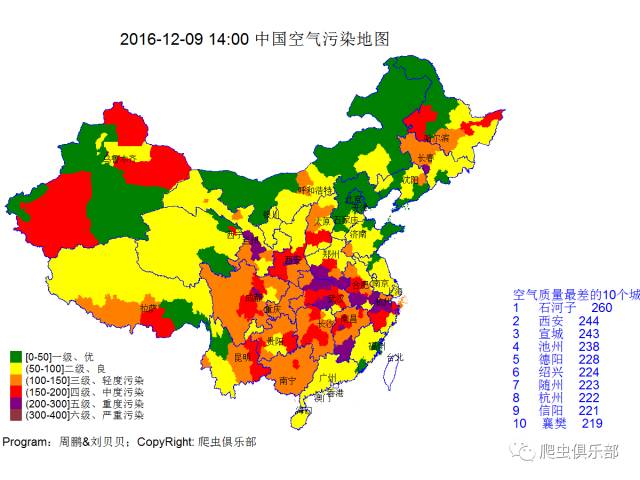
今天点名批评

湖北

 

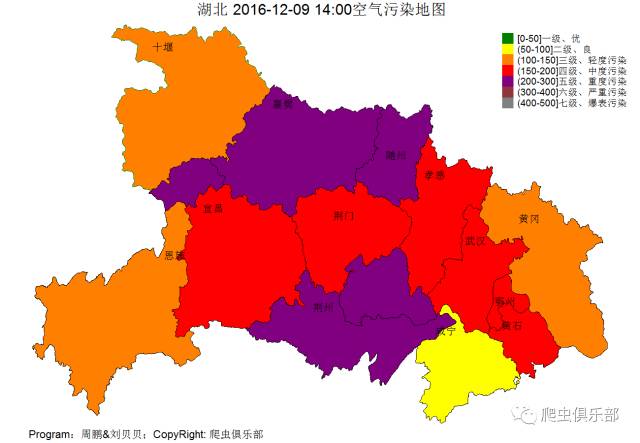
以上就是今天小编与大家分享的全部内容了，如果各位看官喜欢今天分享的内容，不要吝啬你的打赏哦!想了解更多的Stata知识，请继续关注我们的公众号，我们将在后期继续分享更多的干货！

应广大粉丝要求，爬虫俱乐部的推文公众号打赏功能可以开发票啦，累计打赏超过1000元我们即可给您开具发票，发票类别为“咨询费”。用心做事，只为做您更贴心的小爬虫。第一批发票已经寄到各位小主的手中，大家快来给小爬虫打赏呀~

编辑by张欢

欢迎关注爬虫俱乐部