定积分是 函数的一种特定结构总合式的极限，这种极限不仅是计算区域面积或度量几何体的数学工具，而且也是计算许多实际问题的重要工具。我们可以应用定积分来计算一 些常见的几何量、物理量以及经济参数。当计算某个定积分时，若我们能够得到f(x)的原函数，我们就可以利用牛顿-莱布尼茨公式计算定积分的值。然而，在 很多情况下，由于f(x)的形式太复杂，我们很难推导原函数，此时我们求助于数值积分，即：曲线和坐标轴围成曲边形的面积。今天分享的内容是在stata中如何用随机模拟法计算数值积分，下面我们通过具体的实例给大家展示。

首先我们绘制出两曲线相交所围成的曲边形，具体代码如下：

set scheme s1color

clear

set obs 5000

gen x=uniform()*4+(-1.5)

gen y1=x^2

gen y2=x+2

gen low=min(y1,y2)

gen high=max(y1,y2)

twoway rarea low y1 x, sort fcolor(white) lcolor(white) || rarea low y2 x ,sort fcolor(green) lcolor(black)

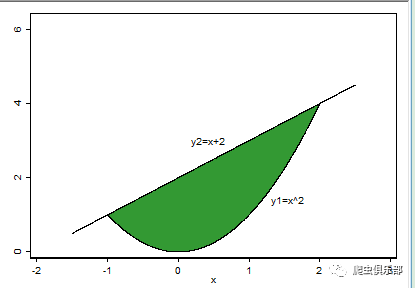
可 以得到交点的横坐标为：-1和2，所以面积为从-1到2上的定积分(x+2-x^2)，而且被积函数很容易找到原函数，所以解得：面积为9/2。现在我们 用投点法进行随机模拟计算该定积分。首先，可以计算出被积函数在(-1,2)上先增后减，最大值为9/4，所以我们所选取的覆盖曲边梯形的矩形的高为3， 模拟程序如下：

clear

set seed 1234567

set obs 1000

gen u1=uniform()*3+(-1)   //生成(-1,2)上满足均匀分布的随机变量u1

gen u2=uniform()*3     //生成(0,3)上满足均匀分布的随机变量u2

gen n=(u2<u1+2-u1^2)   //生成虚拟变量n,若随机点数落入积分区域内为1.否则为0

qui sum n    //n的平均值正好表示落入积分区域内点数除以总数

dis "acreage=" (2+1)*3*r(mean)

结果如下：

上 面的问题除了用投点法之外，我们还可以用平均法计算定积分。根据大样本理论，数学期望可以用大样本的平均值进行逼近，因此如果能模拟密度函数为f(x)的 随机变量X，我们就可以得到随机变量Y=g(x)，然后用对应的Y的样本平均值乘以上下限之差还原定积分，所得结果作为定积分的近似即可。程序如下：

clear

set obs 1000

set seed 1234567

gen x = uniform()*3+(-1)   //生成(-1,2)上满足均匀分布的随机变量x

gen y = x+2-x^2

qui sum y

disp "acreage" 3*r(mean)   //求平均值时，在定积分中乘了x的密度函数，此时要还原为最初的定积分

结果如下：

可以发现上述两种方法，在相同的初值的情况下，得到的定积分近似值都与定积分的真实值相差不远，若想得到更为精确地的模拟值，只需将上述程序重复多次，程序如下：

clear

set more off

set seed 1234567

capture postclose integration   //运用post文件,若文件integration打开就关上，否则忽略此行

postfile integration I using d:\I,replace   //定义post文件integration，包含的变量名为i，保存在d盘

forval i=1(1)100{     //执行循环100次

   qui set obs 1000

   gen x = uniform()*3+(-1)

   gen y = x+2-x^2

   qui sum y

   scalar i=3*r(mean)    //定义一次实验的积分值

   post integration (i)    //调用post文件integration，将i值储存在变量I中

   clear

 }

postclose Integration    //结束post文件

use d:\I    //调用所储存的数据文件

qui sum I

dis "Integration" = r(mean)

结果如下：

此时，得到的积分值就与真实值非常接近了！用stata进行定积分计算，跟着小编你学会了吗？

接下来是空气质量报告

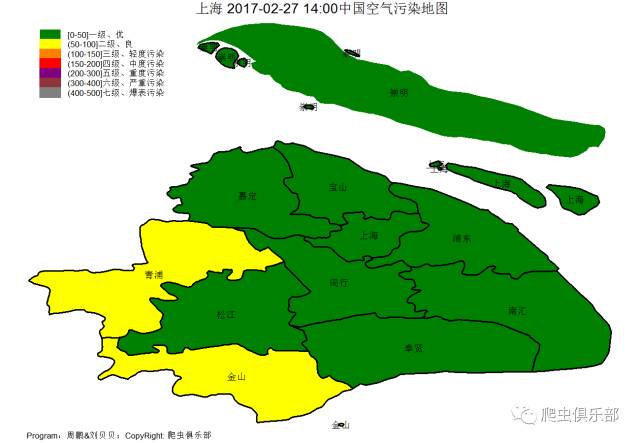
全国空气质量如下

今日全国各地姹紫嫣红

上海这样的空气已经是数一数二的好啦

以上就是今天给大家分享的内容了，说得好就赏个铜板呗！有钱的捧个钱场，有人的捧个人场~，点赞打赏随您心意，么么哒~

应广大粉丝要求，爬虫俱乐部的推文公众号打赏功能可以开发票啦，累计打赏超过1000元我们即可给您开具发票，发票类别为“咨询费”。用心做事，只为做您更贴心的小爬虫。第一批发票已经寄到各位小主的手中，大家快来给小爬虫打赏呀~

文字编辑：徐苾雯

技术总编：刘贝贝

往期推文推荐：

1.合并输出回归结果和其他检验结果——esttab和estadd

2.关于RTF你不知道的命令

3.关于RTF你不知道的命令之番外篇

4.免费事件研究，一片片从邮局寄来

5.免费的股价同步性，一片片从邮局寄来

6.Stata叫你回家听音乐了！

7.一言不合就用stata写邮件（Outlook/Foxmail）

8.玩转stata之调用浏览器

9.I have a Stata, I have a python

10.I have a Stata, I have a Python之二——pdf转word

此外，欢迎大家踊跃投稿，介绍一些关于stata的数据处理和分析技巧。

投稿邮箱：xueyuan19920310@163.com

投稿要求：
1）必须原创，禁止抄袭；
2）必须准确，详细，有例子，有截图；
注意事项：
1）所有投稿都会经过本公众号运营团队成员的审核，审核通过才可录用，一经录用，会在该推文里为作者署名，并有赏金分成。
2）邮件请注明投稿，邮件名称为“投稿”+“推文名称”。
3）应广大读者要求，现开通有偿问答服务，如果大家遇到关于stata分析数据的问题，可以在公众号中提出，只需支付少量赏金，我们会在后期的推文里给予解答。