（本文整理于由李春涛教授、张璇副教授编写的《随机模拟与金融数据处理Stata教程》）

Monte Carlo模拟因摩纳哥公国著名的 赌城Monte Carlo而得名。MonteCarlo方法，又称随机抽样或统计试验方法，是一种随机模拟方法，是使用随机数（或更常见的伪随机数）来解决很多计算问题 的方法。其原理是通过大量随机样本，去了解一个系统，进而得到所要计算的值。为象征地表明这一方法的概率统计特征，故借用赌城Monte Carlo命名。MonteCarlo方法广泛应用于数学、物理、化学、工程、经济金融等领域。

（1）mod(x,y)函数：

给出x除以y之后的余数，即：mod(x,y) = x - y*int(x/y)，举例：

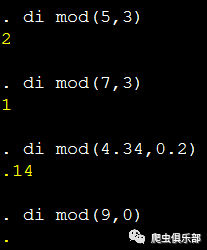
值得注意的是： mod(9,0) = .，即：结果为空值，因为9除以0无意义。

（2）runiform()函数：

用来生成[0,1)区间上均匀分布的伪随机数。注：以前该函数命令为uniform()，二者通用。

之所以称之为“伪随机”数，顾名思义，它并非真正绝对的是随机产生，只是相对随机，表面看似随机，又因其可以通过大多数统计随机检验，所以可以近似模拟随机。

（详见《随机模拟与金融数据处理Stata教程》）

clear

set more off

set obs 1000  //设置1000个观测值，试图生成1000个伪随机数

local m = 9^13-9      

local a = 7^12-2 //设置参数a,m，不同参数选取会对随机数的生成产生影响

gen int y = 1 if _n==1  //设置y的初值为1

gen t = _n      //生成观测值序号

replace y = mod(`a'*y[_n-1],`m')  if _n>1  //前一行的y乘以参数`a',然后除以`m'之后的余数，此余数即为给y的赋值

gen x = y/`m'   //生成伪随机变量（我们生成(0,1)上的随机数）

sum x         //（见图1）

twoway scatter x t    //绘制关于x、t的散点图（见图2）

图1:伪随机数x的描述性统计

根据图1，可以看到，生成(0-1)之间的1000个伪随机数中，最小值几乎为0，最大值约为0.9997，几乎为1，均值约为0.49，接近0.5，标准差约0.28。下面再来看图2，可以很直观地看到，这些点“随机”地分布在关于x、t的散点图上面。

图2:线性同余法生成伪随机数的散点图

（用runiform()函数生成[0,1)区间上均匀分布的伪随机数）

clear

set obs 1000

*set seed 1234567     //此行为可选行，设置初值，可以反复生成固定结果的伪随机数

gen x = runiform()    //生成[0,1)区间上的均匀分布的随机数

gen t =_n

sum x                 //见图3

twoway scatter x t           //见图4

图3:伪随机数x的描述性统计

类似图1，在图3中，生成(0-1)之间的1000个伪随机数中，最小值约为0.0007，几乎为0，最大值约为0.9992，几乎为1，均值接近0.5，标准差约0.29。下面图4中，可以直观地看到， 各个点“随机”地分布在散点图上。

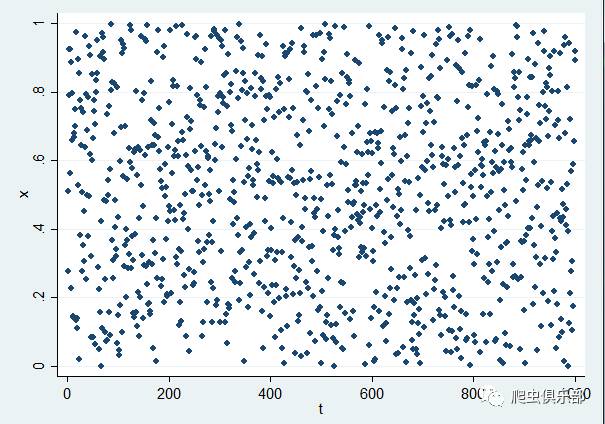
图4: runiform()函数生成伪随机数散点图

除了生成0-1之间的伪随机数之外，还可以生成其他区间上的伪随机数，下面我们来生成0-100之间的伪随机整数。

clear

set more off

set obs 1000

gen a = int(uniform()*10^2)           //生成[0,100)区间上的均匀分布的随机整数（也可以不取整，去掉int()函数生成0-100之间的小数）

sum a           //见图5

gen t=_n

twoway scatter a t               //见图6

图5：伪随机数a的描述性统计

在图5中，生成了[0,100)上的1000个伪随机整数，最小值为0，最大值为99，均值约49.95，接近50，标准差约28.59。下面图6中，可以直观地看到，伪随机数a随着t的变化，“随机”地分布在关于x、t的散点图上面。

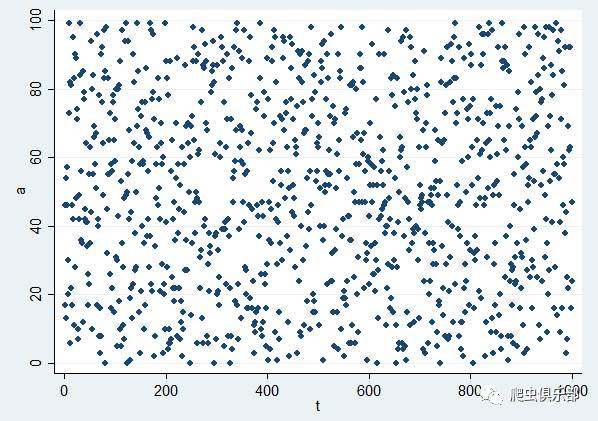
图6:伪随机数的散点图

蒙特卡罗方法

蒙特卡罗方法于20世纪40年代美国在第二次世界大战中研制原子弹的 “曼哈顿计划”计划的成员S.M.乌拉姆和J.冯·诺伊曼首先提出。数学家冯·诺伊曼用驰名世界的赌城—摩纳哥的MonteCarlo—来命名这种方法， 为它蒙上了一层神秘色彩。在这之前，蒙特卡罗方法就已经存在。1777年，法国数学家布丰（Georges Louis Leclere de Buffon，1707—1788）提出用投针实验的方法求圆周率π。这被认为是蒙特卡罗方法的起源。Monte Carlo方法创始人主要是这四位：Stanislaw Marcin Ulam, Enrico Fermi, John von Neumann（学计算机的肯定都认识这个牛人吧）和 Nicholas Metropolis。

风情公国摩纳哥

摩纳哥公国（法语：Principautéde Monaco，英语：The Principality of Monaco），简称“摩纳哥”，是位于欧洲西南部的一个城邦国家，是欧洲两个公国之一（另一个是列支敦士登），也是世界第二小的国家（面积最小的是梵蒂冈），总面积为1.98平方公里，世人称之为“赌博之国”、“袖珍之国”、“邮票小国”。 蒙特卡洛是摩纳哥公国的一座城市，是世界著名的赌城，是摩纳哥的标志，世界三大赌城之一（美国超级赌城拉斯维加斯与号称东方拉斯维加斯的中国澳门）。蒙特卡罗的赌业，海洋博物馆的奇观，格蕾丝王妃的下嫁，都为这个小国增添了许多传奇的色彩…… 

 格蕾丝王妃

 格蕾丝王妃是摩纳哥历史上绝无仅有的国家名片，也是欧洲王室一抹最浓重的童话。 优雅美丽的好莱坞女星格蕾斯·凯莉和雷尼尔王子“童话般爱情”，这是一段牵动全球的罗曼史，一个美国电影皇后与欧洲王子的故事，他们曾经在地中海畔小山顶的王宫内过着神仙眷侣的生活。曾有人赞誉雷尼尔的这段爱情是20世纪最动人的爱情。这场爱情至真至善、至伟至美。

奥斯卡影后格蕾丝凯利

格蕾丝·凯利（Grace Kelly），1929年11月12日出生于费城，美国影视演员。

1955年，她凭借在《乡下姑娘》的表演获得第27届奥斯卡最佳女主角奖。

1956年，格蕾丝·凯利与雷尼尔三世结婚，成为摩纳哥王妃。

参考资料：

1.《随机模拟与金融数据处理Stata教程》（李春涛、张璇著）

2.http://baike.baidu.com/view/1675475.htm?fr=ala0_1

3.http://baike.baidu.com/view/42460.htm?fr=ala0_1_1

4.http://wiki.mbalib.com/wiki/%E8%92%99%E7%89%B9%E5%8D%A1%E7%BD%97%E6%96%B9%E6%B3%95

5.http://baike.baidu.com/item/%E8%92%99%E7%89%B9%E5%8D%A1%E6%B4%9B/61817?fromtitle=Monte+Carlo&fromid=74910&type=syn

6、http://baike.baidu.com/item/摩纳哥

7、http://baike.baidu.com/view/6359248.htm

8、http://baike.baidu.com/item/格蕾丝·凯利/10574420